11722. Rectangle cutting

A rectangle of size a × b is given. Your task is to cut it into squares. In one move, you can select one of the rectangles and split it into two new rectangles so that all side lengths remain integers. Determine the minimum number of moves required to complete this task.

Input. Two integers a and b (1 ≤ a, b ≤ 500).

Output. Print the minimum number of moves required to cut the rectangle into squares.

Sample input 1	Sample output 1
3 5	3
Sample input 2	Sample output 2
5 10	1

SOLUTION

dynamic programming

Algorithm analysis

Let f(a, b) be the minimum number of moves required to cut a rectangle of size a × b into squares. We’ll store this value in the cell dp[a][b].

If the rectangle is already a square (a = b), no cuts are needed, so f(a, a) = 0.

A rectangle a × b can be cut either vertically or horizontally. Let’s first consider a vertical cut.

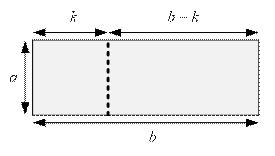
With a vertical cut, the rectangle a × b is divided into two rectangles: a × k and a × (b – k). For the resulting rectangles to be non-degenerate, the condition 1 ≤ k < b must hold. Then recursively solve the problem for each of these two rectangles and add 1 to the result, as we made one vertical cut. We choose such a k that minimizes the sum f(a, k) + f(a, b – k) + 1:

f(a, b) =

For a horizontal cut, we get a similar formula:

f(a, b) =

It remains to choose the minimum value among these two options.

Example

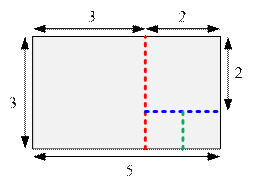
In the first test, 3 cuts are required:

· The first cut divides the 3 × 5 rectangle into 3 × 3 and 2 × 3;

· The second cut divides the 2 × 3 rectangle into 2 × 2 and 2 × 1;

· The third cut divides the 2 × 1 rectangle into 1 × 1 and 1 × 1;

Algorithm implementation

Let’s declare constants and the array.

#define MAX 501

#define INF 0x3F3F3F3F

int dp[MAX][MAX];

The function f(a, b) returns the minimum number of moves required to cut a rectangle of size a × b into squares.

int f(int a, int b)

{

If the rectangle is already a square (a = b), no cuts are needed.

if (a == b) return 0;

If the value of f(a, b) is not computed (dp[a][b] = ∞), compute it.

if (dp[a][b] == INF)

{

Perform all possible vertical cuts.

for (int k = 1; k < b; k++)

dp[a][b] = min(dp[a][b], f(a, k) + f(a, b - k) + 1);

Perform all possible horizontal cuts.

for (int k = 1; k < a; k++)

dp[a][b] = min(dp[a][b], f(k, b) + f(a - k, b) + 1);

}

Return the result f(a, b) = dp[a][b].

return dp[a][b];

}

The main part of the program. Read the dimensions of the rectangle a and b.

scanf("%d %d", &a, &b);

Compute and print the answer.

memset(dp, 0x3F, sizeof(dp));

printf("%d\n", f(a, b));